Today is the day 😃 “Why?” you might ask. The reason is that today we’re wrapping up our discussion of arithmetic expressions (well, almost) by adding parenthesized expressions to our grammar and implementing an interpreter that will be able to evaluate parenthesized expressions with arbitrarily deep nesting, like the expression 7 + 3 * (10 / (12 / (3 + 1) - 1)).

今天就是这个日子:)“为什么?”你可能会问。原因是，今天我们结束了对算术表达式(嗯，几乎)的讨论，我们在grammar中添加了括号表达式，并实现了一个解释器，它可以用任意深度的嵌套对括号表达式求值，比如表达式7 + 3 * (10/(12/(3 + 1)-1))。

Let’s get started, shall we?

我们开始吧？

First, let’s modify the grammar to support expressions inside parentheses. As you remember from Part 5, the factor rule is used for basic units in expressions. In that article, the only basic unit we had was an integer. Today we’re adding another basic unit - a parenthesized expression. Let’s do it.

首先，让我们修改grammar以支持括号内的表达式。正如你在第5部分中所记得的，factor 规则用于表达式中的基本单位。在那篇文章中，我们唯一的基本单位是一个整数。今天我们要添加另一个基本单元——括号表达式。我们开始吧。

Here is our updated grammar:

下面是我们最新的grammar:

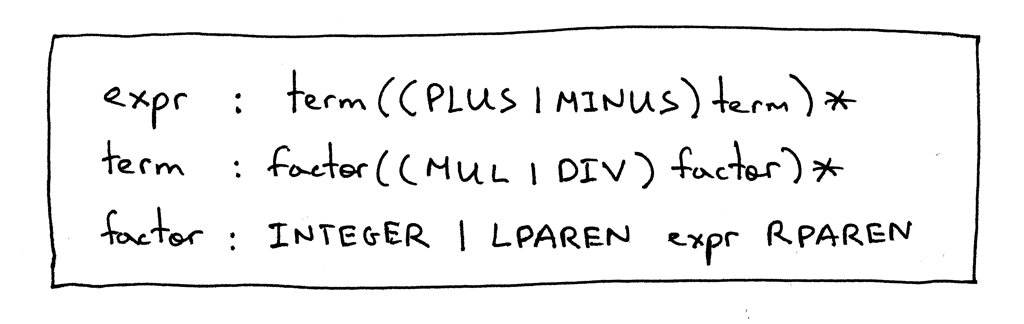
The expr and the term productions are exactly the same as in Part 5 and the only change is in the factor production where the terminal LPAREN represents a left parenthesis ‘(‘, the terminal RPAREN represents a right parenthesis ‘)’, and the non-terminal expr between the parentheses refers to the expr rule.

Expr 和 term 两个产生式与第5部分中的完全相同，唯一的变化是factor 产生式，其中终结符 LPAREN 表示左括号“(”，终结符 RPAREN 表示右括号‘)’，括号之间的非终结符 expr 表示 expr 产生式。

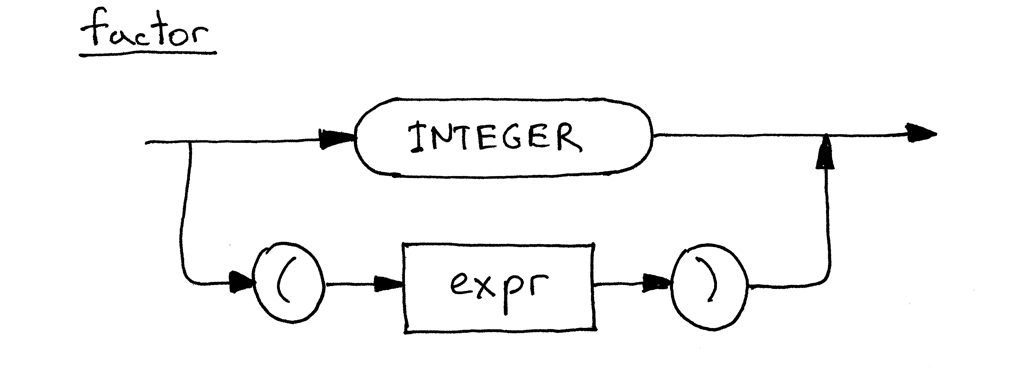
Here is the updated syntax diagram for the factor, which now includes alternatives:

下面是更新后的factor的syntax图，现在包含了其他选项:

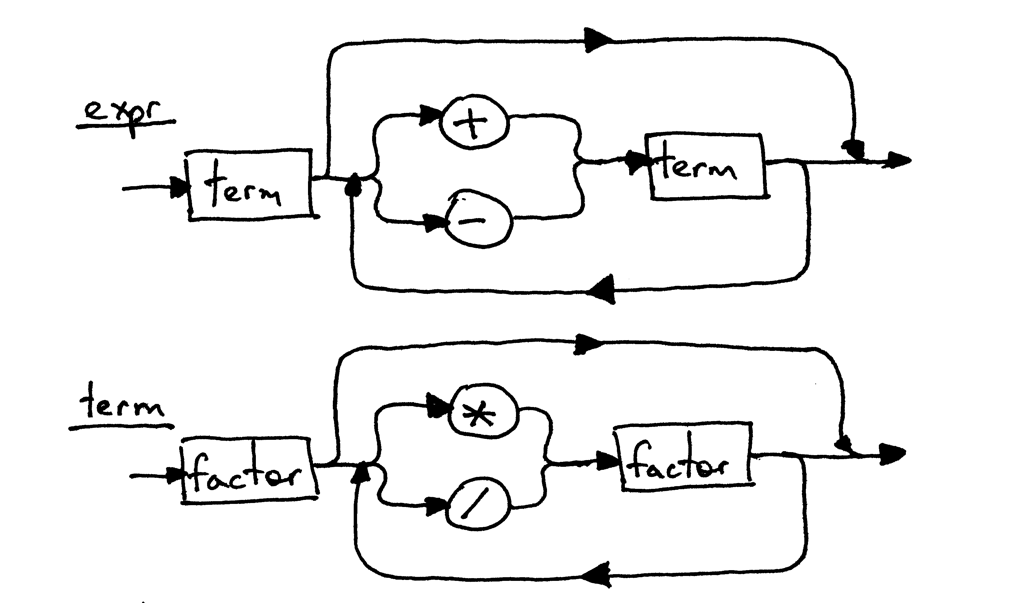
Because the grammar rules for the expr and the term haven’t changed, their syntax diagrams look the same as in Part 5:

因为 expr 和 term 的grammar规则没有改变，它们的syntax图看起来和第5部分一样:

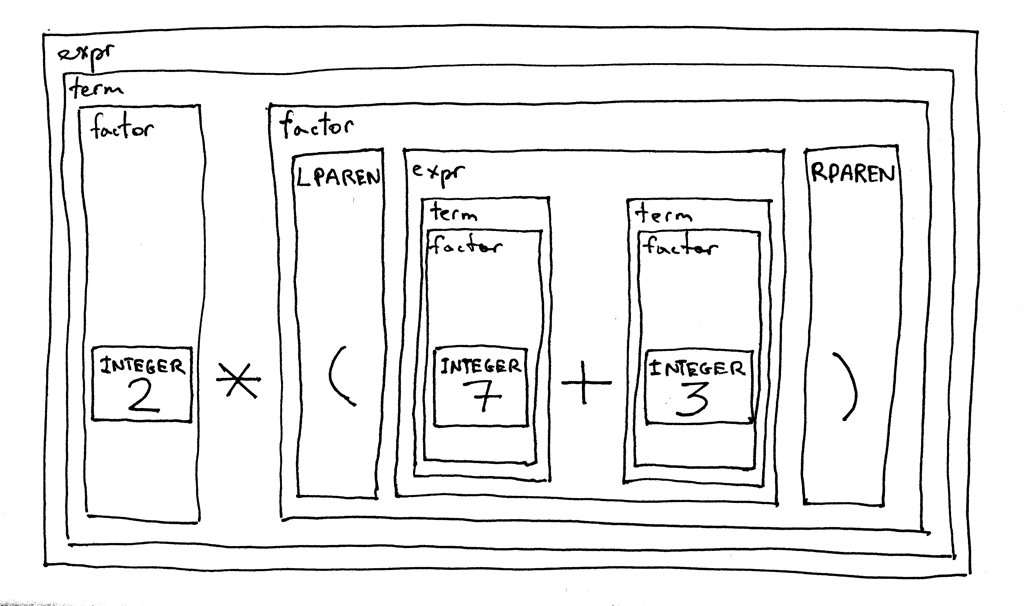
Here is an interesting feature of our new grammar - it is recursive. If you try to derive the expression 2 * (7 + 3), you will start with the expr start symbol and eventually you will get to a point where you will recursively use the expr rule again to derive the (7 + 3) portion of the original arithmetic expression.

这是我们新grammar的一个有趣的特点——它是递归的。如果您尝试派生表达式2 * (7 + 3) ，那么您将从 expr 起始符号开始，最终您将到达一个点，会再次递归地使用 expr 规则派生原始算术表达式的(7 + 3)部分。

Let’s decompose the expression 2 * (7 + 3) according to the grammar and see how it looks:

让我们根据grammar分解表达式2 * (7 + 3) ，看看它是什么样的:

A little aside: if you need a refresher on recursion, take a look at Daniel P. Friedman and Matthias Felleisen’s The Little Schemer book - it’s really good.

顺便说一句: 如果你需要复习一下递归，可以看一下Daniel P. Friedman和 Matthias Felleisen 的《The Little Schemer》-这本书真的很不错。

Okay, let’s get moving and translate our new updated grammar to code.

好了，让我们开始吧，把新更新的grammar翻译成代码。

The following are the main changes to the code from the previous article:

以下是对上一篇文章代码的主要修改:

  1. The Lexer has been modified to return two more tokens: LPAREN for a left parenthesis and RPAREN for a right parenthesis.
    • 对Lexer进行了修改，以返回另外两个标记:LPAREN(左括号)和RPAREN(右括号)。
  2. The Interpreter‘s factor method has been slightly updated to parse parenthesized expressions in addition to integers.
    • 解释器的factor方法略有更新，除了解析整数外，还可以解析圆括号表达式。

Here is the complete code of a calculator that can evaluate arithmetic expressions containing integers; any number of addition, subtraction, multiplication and division operators; and parenthesized expressions with arbitrarily deep nesting:

下面是一个计算器的完整代码，它可以计算包含整数的算术表达式; 任意数量的加、减、乘、除运算符; 以及任意深度嵌套的括号表达式:

# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, LPAREN, RPAREN, EOF = (
    'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', '(', ')', 'EOF'
)


class Token(object):
    def __init__(self, type, value):
        self.type = type
        self.value = value

    def __str__(self):
        """String representation of the class instance.

        Examples:
            Token(INTEGER, 3)
            Token(PLUS, '+')
            Token(MUL, '*')
        """
        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self):
        return self.__str__()


class Lexer(object):
    def __init__(self, text):
        # client string input, e.g. "4 + 2 * 3 - 6 / 2"
        self.text = text
        # self.pos is an index into self.text
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Invalid character')

    def advance(self):
        """Advance the `pos` pointer and set the `current_char` variable."""
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None  # Indicates end of input
        else:
            self.current_char = self.text[self.pos]

    def skip_whitespace(self):
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self):
        """Return a (multidigit) integer consumed from the input."""
        result = ''
        while self.current_char is not None and self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        """Lexical analyzer (also known as scanner or tokenizer)

        This method is responsible for breaking a sentence
        apart into tokens. One token at a time.
        """
        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()
                continue

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())

            if self.current_char == '+':
                self.advance()
                return Token(PLUS, '+')

            if self.current_char == '-':
                self.advance()
                return Token(MINUS, '-')

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            if self.current_char == '(':
                self.advance()
                return Token(LPAREN, '(')

            if self.current_char == ')':
                self.advance()
                return Token(RPAREN, ')')

            self.error()

        return Token(EOF, None)


class Interpreter(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # set current token to the first token taken from the input
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        # compare the current token type with the passed token
        # type and if they match then "eat" the current token
        # and assign the next token to the self.current_token,
        # otherwise raise an exception.
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """factor : INTEGER | LPAREN expr RPAREN"""
        token = self.current_token
        if token.type == INTEGER:
            self.eat(INTEGER)
            return token.value
        elif token.type == LPAREN:
            self.eat(LPAREN)
            result = self.expr()
            self.eat(RPAREN)
            return result

    def term(self):
        """term : factor ((MUL | DIV) factor)*"""
        result = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
                result = result * self.factor()
            elif token.type == DIV:
                self.eat(DIV)
                result = result // self.factor()

        return result

    def expr(self):
        """Arithmetic expression parser / interpreter.

        calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
        22

        expr   : term ((PLUS | MINUS) term)*
        term   : factor ((MUL | DIV) factor)*
        factor : INTEGER | LPAREN expr RPAREN
        """
        result = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
                result = result + self.term()
            elif token.type == MINUS:
                self.eat(MINUS)
                result = result - self.term()

        return result


def main():
    while True:
        try:
            text = input('calc> ')
        except EOFError:
            break
        if not text:
            continue
        lexer = Lexer(text)
        interpreter = Interpreter(lexer)
        result = interpreter.expr()
        print(result)


if __name__ == '__main__':
    main()

Save the above code into the calc6.py file, try it out and see for yourself that your new interpreter properly evaluates arithmetic expressions that have different operators and parentheses.

将上面的代码保存到 calc6.py 文件中，尝试一下，看看你的新解释器能否正确地计算具有不同运算符和括号的算术表达式。

Here is a sample session:

下面是一个例子:

$ python calc6.py
calc> 3
3
calc> 2 + 7 * 4
30
calc> 7 - 8 / 4
5
calc> 14 + 2 * 3 - 6 / 2
17
calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
22
calc> 7 + 3 * (10 / (12 / (3 + 1) - 1)) / (2 + 3) - 5 - 3 + (8)
10
calc> 7 + (((3 + 2)))
12

And here is a new exercise for you for today:

下面是今天的一个新练习:

  • Write your own version of the interpreter of arithmetic expressions as described in this article. Remember: repetition is the mother of all learning.
    • 如本文所述，编写你自己版本的算术表达式解释器。记住: 重复是学习之母。

Hey, you read all the way to the end! Congratulations, you’ve just learned how to create (and if you’ve done the exercise - you’ve actually written) a basic recursive-descent parser / interpreter that can evaluate pretty complex arithmetic expressions.

嘿，你从头读到尾了！恭喜你，你刚刚学会了如何创建一个基本的递归下降解析器/解释器(如果你已经完成了这个练习的话——你实际上已经编写了) ，它可以计算非常复杂的算术表达式。

In the next article I will talk in a lot more detail about recursive-descent parsers. I will also introduce an important and widely used data structure in interpreter and compiler construction that we’ll use throughout the series.

在下一篇文章中，我将更详细地讨论递归下降解析器。我还将介绍一种在解释器和编译器构造中广泛使用的重要数据结构，我们将在整个系列中使用这种结构。

Stay tuned and see you soon. Until then, keep working on your interpreter and most importantly: have fun and enjoy the process!

请继续关注，回头见。在那之前，继续为你的解释器工作，最重要的是: 享受这个过程！

Here is a list of books I recommend that will help you in your study of interpreters and compilers:

下面是我推荐的一些书籍，它们可以帮助你学习解释器和编译器:

  1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
    语言实现模式: 创建您自己的特定领域和通用编程语言(实用程序员)
  2. Writing Compilers and Interpreters: A Software Engineering Approach
    编写编译器和解释器: 一种软件工程方法
  3. Modern Compiler Implementation in Java
    现代编译器在 Java 中的实现
  4. Modern Compiler Design
    现代编译器设计
  5. Compilers: Principles, Techniques, and Tools (2nd Edition)
    编译器: 原理、技术和工具(第二版)

All articles in this series: