Have you been passively learning the material in these articles or have you been actively practicing it? I hope you’ve been actively practicing it. I really do 😃

你是被动地学习这些文章中的内容，还是主动地练习？我希望你已经积极练习过了。我真的是这么想的:)

Remember what Confucius said?

还记得孔子说过什么吗？

“I hear and I forget.”

“I see and I remember.”

“I do and I understand.”

其实是荀子说的：“不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之。”

In the previous article you learned how to parse (recognize) and interpret arithmetic expressions with any number of plus or minus operators in them, for example “7 - 3 + 2 - 1”. You also learned about syntax diagrams and how they can be used to specify the syntax of a programming language.

在前一篇文章中，你学习了如何解析（识别）和解释带有任意数量的加减运算符的算术表达式，例如“7-3 + 2-1”。你还了解了语法（syntax）图，以及如何使用它们指定编程语言的语法。

Today you’re going to learn how to parse and interpret arithmetic expressions with any number of multiplication and division operators in them, for example “7 * 4 / 2 * 3”. The division in this article will be an integer division, so if the expression is “9 / 4”, then the answer will be an integer: 2.

今天，你将学习如何解析和解释带有任意数量乘法和除法运算符的算术表达式，例如“7 * 4/2 * 3”。本文中的除法是整数除法，因此如果表达式是“9/4”，那么答案将是整数: 2。

I will also talk quite a bit today about another widely used notation for specifying the syntax of a programming language. It’s called context-free grammars (grammars, for short) or BNF (Backus-Naur Form). For the purpose of this article I will not use pure BNF notation but more like a modified EBNF notation.

今天我还将相当详细地讨论另一种广泛使用的用于指定编程语言语法的符号。它被称为上下文无关文法(简称grammar)或 BNF (Backus-Naur Form)。基于本文的目的，我将不使用纯 BNF 符号，而更像是一种修改后的 EBNF 符号。

Here are a couple of reasons to use grammars:

以下是使用grammar的几个原因:

  1. A grammar specifies the syntax of a programming language in a concise manner. Unlike syntax diagrams, grammars are very compact. You will see me using grammars more and more in future articles.
    • grammar以简洁的方式指定了编程语言的syntax。与语法（syntax）图不同，grammar非常紧凑。在以后的文章中，你会看到我越来越多地使用grammar。
  2. A grammar can serve as great documentation.
    • grammar可以作为很好的文档
  3. A grammar is a good starting point even if you manually write your parser from scratch. Quite often you can just convert the grammar to code by following a set of simple rules.
    • 即使你从头开始手动编写解析器，grammar也是一个很好的起点。通常情况下，你只需遵循一组简单的规则就可以将grammar转换为代码。
  4. There is a set of tools, called parser generators, which accept a grammar as an input and automatically generate a parser for you based on that grammar. I will talk about those tools later on in the series.
    • 有一组名为”Parser生成器”的工具，接受grammar作为输入，并根据该grammar自动为您生成解析器。稍后会谈论那些工具。

Now, let’s talk about the mechanical aspects of grammars, shall we?

现在，让我们来谈谈grammar，好吗？

Here is a grammar that describes arithmetic expressions like “7 * 4 / 2 * 3” (it’s just one of the many expressions that can be generated by the grammar):

下面是一个描述算术表达式的grammar，比如“7 * 4/2 * 3”(这只是由grammar生成的众多表达式之一) :

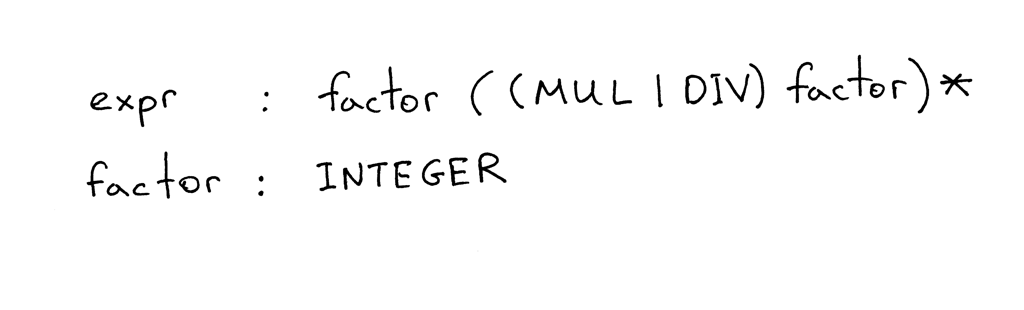
A grammar consists of a sequence of rules, also known as productions. There are two rules in our grammar:

grammar由一系列的规则（也称为_productions（产生式）_）组成。我们的grammar有两个规则:

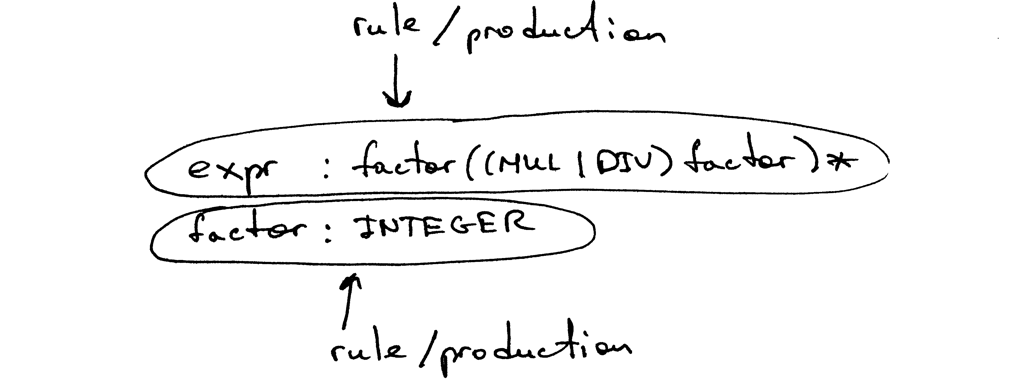
A rule consists of a non-terminal, called the head or left-hand side of the production, a colon, and a sequence of terminals and/or non-terminals, called the body or right-hand side of the production:

一个规则由一个非终结符(称为production的head或left-hand side)、冒号和一系列终结符/非终结符(称为production的body或right-hand side)组成:

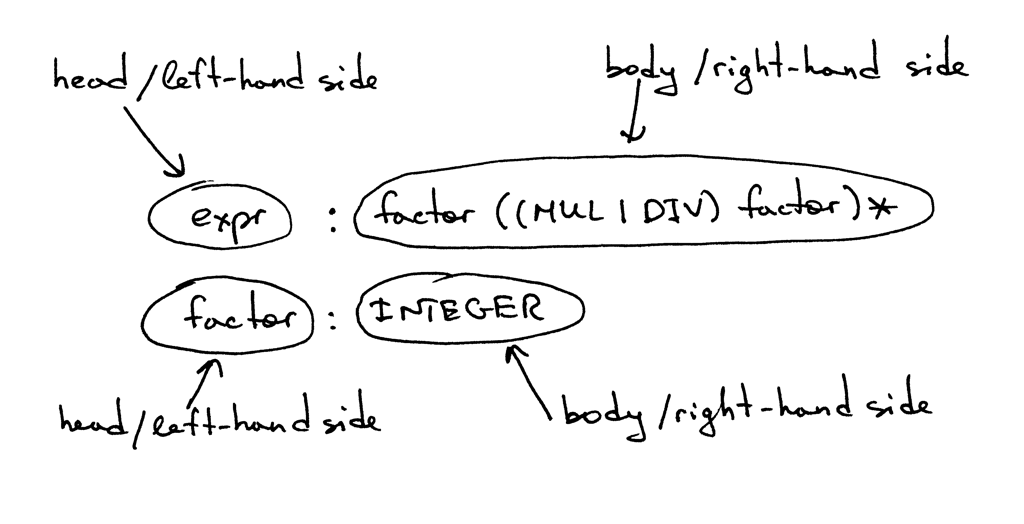
In the grammar I showed above, tokens like MUL, DIV, and INTEGER are called terminals and variables like expr and factor are called non-terminals. Non-terminals usually consist of a sequence of terminals and/or non-terminals:

在上面展示的grammar中，像 MUL、 DIV 和 INTEGER 这样的token称为终结符，像 expr 和 factor 这样的变量称为非终结符。非终结符通常由一系列终结符和或非终结符组成:

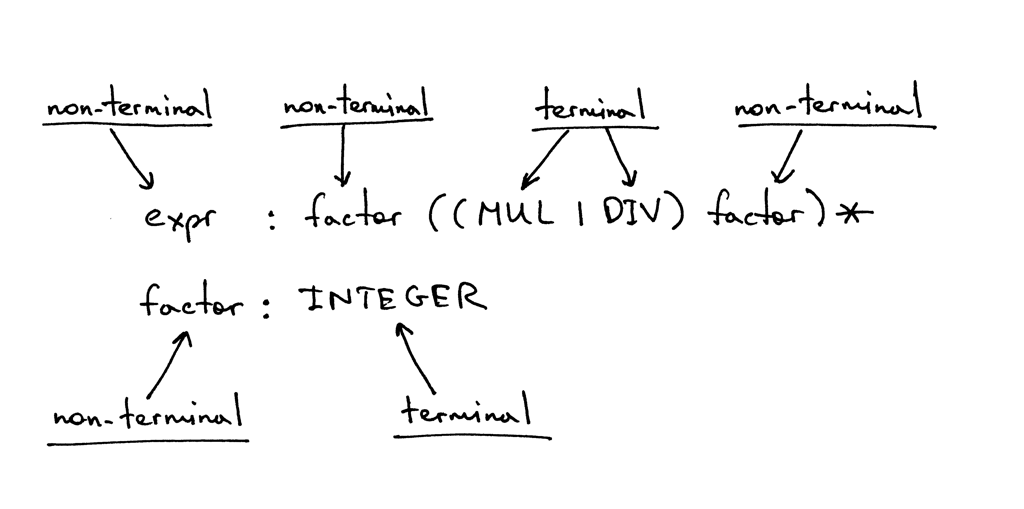
The non-terminal symbol on the left side of the first rule is called the start symbol. In the case of our grammar, the start symbol is expr:

第一条规则左侧的非终结符称为开始符号。在我们的grammar中，开始符号是 expr:

You can read the rule expr as “An expr can be a factor optionally followed by a multiplication or division operator followed by another factor, which in turn is optionally followed by a multiplication or division operator followed by another factor and so on and so forth.”

你可以将规则 expr 解读为“ 一个 expr 可以是一个factor，后面跟一个乘法或除法运算符，然后跟另一个factor，再后面跟一个乘法或除法运算符，再后面跟另一个factor，等等。”

What is a factor? For the purpose of this article a factor is just an integer.

什么是factor? 在本文中，factor只是一个整数。

Let’s quickly go over the symbols used in the grammar and their meaning.

让我们快速回顾一下grammar中使用的符号及其含义。

  • | - Alternatives. A bar means “or”. So (MUL | DIV) means either MUL or DIV.
    • 二选一。或者的意思，所以（MUL｜DIV）意味着要么是MUL，要么是DIV
  • ( … ) - An open and closing parentheses mean grouping of terminals and/or non-terminals as in (MUL | DIV).
    • 开括号和闭括号表示终结符 和或 非终结符 的分组，如(MUL | DIV)。
  • ( … )* - Match contents within the group zero or more times.
    • 匹配组内的内容0次或多次

If you worked with regular expressions in the past, then the symbols |, (), and (…)* should be pretty familiar to you.

如果你过去使用过正则表达式，那么符号 | 、()和(...) * 对你来说应该非常熟悉。

A grammar defines a language by explaining what sentences it can form. This is how you can derive an arithmetic expression using the grammar: first you begin with the start symbol expr and then repeatedly replace a non-terminal by the body of a rule for that non-terminal until you have generated a sentence consisting solely of terminals. Those sentences form a language defined by the grammar.

grammar通过解释该语言可以构成什么样的句子来定义一种语言。这就是使用grammar派生算术表达式的方法: 首先从开始符号 expr 开始，然后用该非终结符的规则body重复替换非终结符，直到生成完全由终结符组成的句子。这些句子构成了由grammar定义的语言。

If the grammar cannot derive a certain arithmetic expression, then it doesn’t support that expression and the parser will generate a syntax error when it tries to recognize the expression.

如果grammar无法派生出某个算术表达式，那么它就不支持该表达式，解析器在尝试识别该表达式时将产生语法错误。

I think a couple of examples are in order. This is how the grammar derives the expression 3:

我认为举几个例子是合理的。
这是grammar如何派生表达式3:

This is how the grammar derives the expression 3 * 7:

这是语法如何派生表达式3 * 7:

And this is how the grammar derives the expression 3 * 7 / 2:

这是语法如何派生表达式3 * 7/2:

Whoa, quite a bit of theory right there!

哇，真是一大堆理论！

I think when I first read about grammars, the related terminology, and all that jazz, I felt something like this:

我想当我第一次读到grammar，相关的术语，以及所有的jazz的时候，我的感觉是这样的:

I can assure you that I definitely was not like this:

我可以向你保证，我绝对不是这样的:

It took me some time to get comfortable with the notation, how it works, and its relationship with parsers and lexers, but I have to tell you that it pays to learn it in the long run because it’s so widely used in practice and compiler literature that you’re bound to run into it at some point. So, why not sooner rather than later? 😃

我花了一些时间来熟悉这个符号，它是如何工作的，以及它与语法分析器和词法分析器的关系，但我必须告诉你，从长远来看，学习它是值得的，因为它在实践和编译文献中被广泛使用，你在某个时候一定会遇到它。那么，为什么不早一点而不是晚一点呢？😃

Now, let’s map that grammar to code, okay?

现在，让我们把grammar映射到代码中，好吗？

Here are the guidelines that we will use to convert the grammar to source code. By following them, you can literally translate the grammar to a working parser:

下面是我们将用来将gramar转换为源代码的指导原则。通过跟随它们，你可以逐字地将grammar翻译成一个可以工作的解析器:

  1. Each rule, R, defined in the grammar, becomes a method with the same name, and references to that rule become a method call: R(). The body of the method follows the flow of the body of the rule using the very same guidelines.
    • 在grammar中定义的每个规则R都成为一个具有相同名称的方法，以及对该规则的引用成为方法调用：R（）。该方法的方法体（即函数内容）使用相同的指导原则去变换规则（产生式）的body。
  2. Alternatives (a1 | a2 | aN) become an if-elif-else statement
    • 或（Alternatives） 变成一个 if-elif-else语句
  3. An optional grouping (…)* becomes a while statement that can loop over zero or more times
    • 一个可选组**(...)***变成一个可循环0次或多次的while语句
  4. Each token reference T becomes a call to the method eat: eat(T). The way the eat method works is that it consumes the token T if it matches the current lookahead token, then it gets a new token from the lexer and assigns that token to the current_token internal variable.
    • 每个token引用T都成为对方法eat: eat(T)的调用。eat方法的工作方式是：如果token T的类型与当前内部变量current_token的类型相匹配，那么它将吃掉token T，然后从lexer获得一个新token，并将该token分配给current_token。

Visually the guidelines look like this:

视觉上的指导原则是这样的:

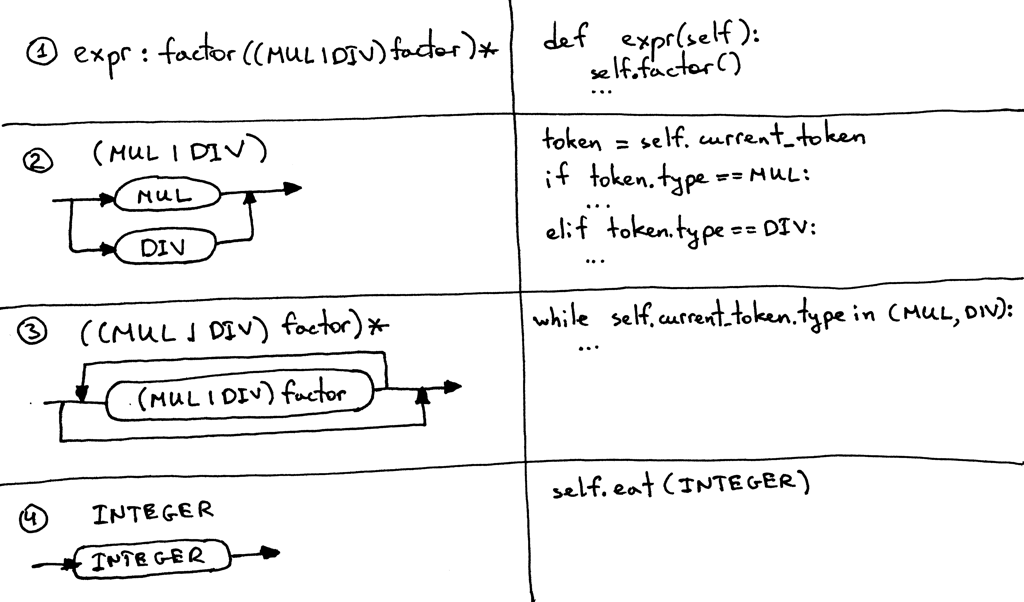
Let’s get moving and convert our grammar to code following the above guidelines.

让我们按照上面的指导方针，将grammar转换为代码。

There are two rules in our grammar: one expr rule and one factor rule. Let’s start with the factor rule (production). According to the guidelines, you need to create a method called factor (guideline 1) that has a single call to the eat method to consume the INTEGER token (guideline 4):

我们的grammar中有两个规: 一个 expr 规则和一个factor规则。让我们从factor规则（产生式production）开始。根据指导原则，您需要创建一个名为 factor （指导原则1）的方法，该方法只调用 eat 方法来使用 INTEGER 标记（指导原则4） :

def factor(self):
    self.eat(INTEGER)

That was easy, wasn’t it?

这很简单，不是吗？

Onward!

前进！

The rule expr becomes the expr method (again according to the guideline 1). The body of the rule starts with a reference to factor that becomes a factor() method call. The optional grouping (…)* becomes a while loop and (MUL | DIV) alternatives become an if-elif-else statement. By combining those pieces together we get the following expr method:

规则 expr 成为 expr 方法(根据指导原则1)。规则体以对 factor 的引用开始，那么expr方法以调用factor()开始。可选的分组(...) * 变成 while 循环，(MUL | DIV)替代项变成 if-elif-else 语句。通过将这些片段组合在一起，我们得到了下面的 expr 方法:

def expr(self):
    self.factor()

    while self.current_token.type in (MUL, DIV):
        token = self.current_token
        if token.type == MUL:
            self.eat(MUL)
            self.factor()
        elif token.type == DIV:
            self.eat(DIV)
            self.factor()

Please spend some time and study how I mapped the grammar to the source code. Make sure you understand that part because it’ll come in handy later on.

请花些时间研究一下我是如何将grammar映射到源代码的。确保你理解了这一部分，因为它迟早会派上用场。

For your convenience I put the above code into the parser.py file that contains a lexer and a parser without an interpreter. You can download the file directly from GitHub and play with it. It has an interactive prompt where you can enter expressions and see if they are valid: that is, if the parser built according to the grammar can recognize the expressions.

为了方便起见，我将上面的代码放到 parser.py 文件中，该文件包含一个 lexer 和一个不带解释器的解析器。你可以直接从 GitHub 下载这个文件并使用它。它有一个交互式提示符，您可以在其中输入表达式并查看它们是否有效：也就是说，如果根据grammar构建的解析器能够识别表达式。

Here is a sample session that I ran on my computer:

下面是我在电脑上运行的一个例子:

$ python parser.py
calc> 3
calc> 3 * 7
calc> 3 * 7 / 2
calc> 3 *
Traceback (most recent call last):
  File "parser.py", line 155, in <module>
    main()
  File "parser.py", line 151, in main
    parser.parse()
  File "parser.py", line 136, in parse
    self.expr()
  File "parser.py", line 130, in expr
    self.factor()
  File "parser.py", line 114, in factor
    self.eat(INTEGER)
  File "parser.py", line 107, in eat
    self.error()
  File "parser.py", line 97, in error
    raise Exception('Invalid syntax')
Exception: Invalid syntax

Try it out!

试试吧！

I couldn’t help but mention syntax diagrams again. This is how a syntax diagram for the same expr rule will look:

我忍不住又提到了语法（syntax）图。下面是同一个 expr 规则的语法图:

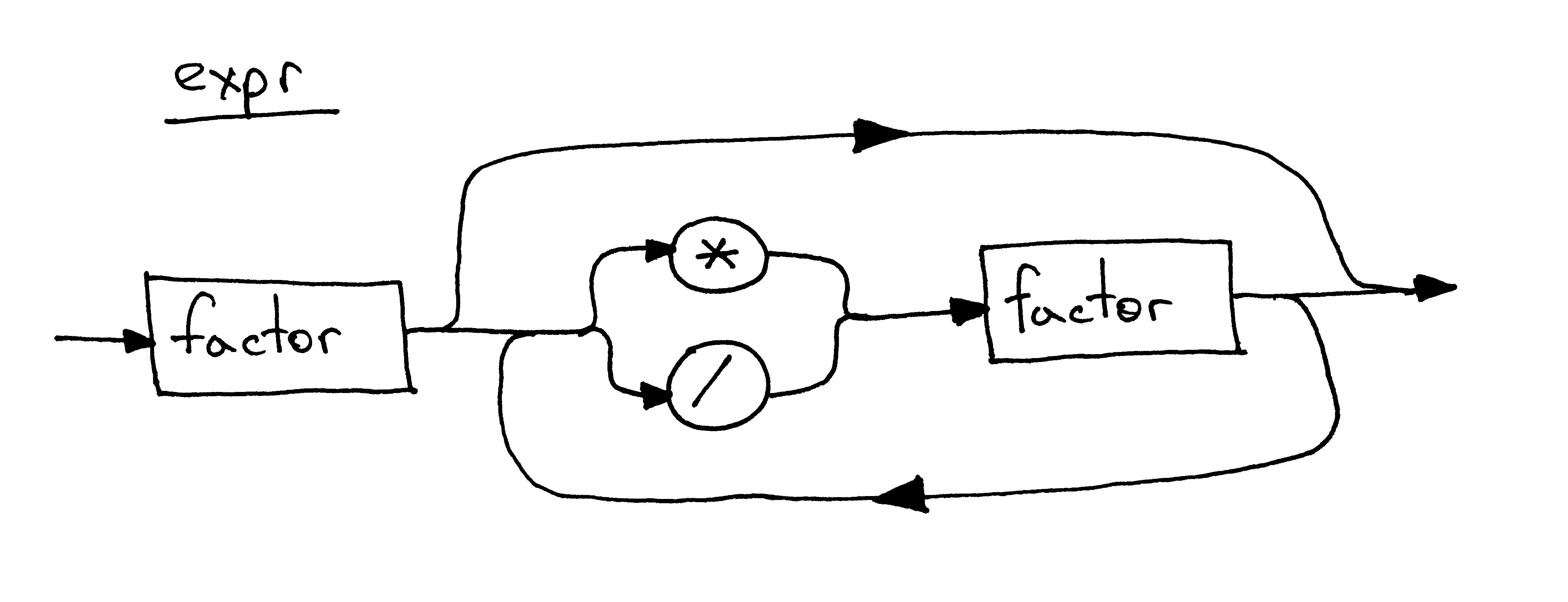
It’s about time we dug into the source code of our new arithmetic expression interpreter. Below is the code of a calculator that can handle valid arithmetic expressions containing integers and any number of multiplication and division (integer division) operators. You can also see that I refactored the lexical analyzer into a separate class Lexer and updated the Interpreter class to take the Lexer instance as a parameter:

是时候深入研究我们新的算术表达式解释器的源代码了。下面是一个计算器的代码，它可以处理包含整数和任意数量的乘法和除法（整数除法）运算符的有效算术表达式。你还可以看到，我将词法分析器重构为一个单独的类 Lexer，并更新了 Interpreter 类，将 Lexer 实例作为参数:

# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, MUL, DIV, EOF = 'INTEGER', 'MUL', 'DIV', 'EOF'


class Token(object):
    def __init__(self, type, value):
        # token type: INTEGER, MUL, DIV, or EOF
        self.type = type
        # token value: non-negative integer value, '*', '/', or None
        self.value = value

    def __str__(self):
        """String representation of the class instance.

        Examples:
            Token(INTEGER, 3)
            Token(MUL, '*')
        """
        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self):
        return self.__str__()


class Lexer(object):
    def __init__(self, text):
        # client string input, e.g. "3 * 5", "12 / 3 * 4", etc
        self.text = text
        # self.pos is an index into self.text
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Invalid character')

    def advance(self):
        """Advance the `pos` pointer and set the `current_char` variable."""
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None  # Indicates end of input
        else:
            self.current_char = self.text[self.pos]

    def skip_whitespace(self):
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self):
        """Return a (multidigit) integer consumed from the input."""
        result = ''
        while self.current_char is not None and self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        """Lexical analyzer (also known as scanner or tokenizer)

        This method is responsible for breaking a sentence
        apart into tokens. One token at a time.
        """
        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()
                continue

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            self.error()

        return Token(EOF, None)


class Interpreter(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # set current token to the first token taken from the input
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        # compare the current token type with the passed token
        # type and if they match then "eat" the current token
        # and assign the next token to the self.current_token,
        # otherwise raise an exception.
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """Return an INTEGER token value.

        factor : INTEGER
        """
        token = self.current_token
        self.eat(INTEGER)
        return token.value

    def expr(self):
        """Arithmetic expression parser / interpreter.

        expr   : factor ((MUL | DIV) factor)*
        factor : INTEGER
        """
        result = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
                result = result * self.factor()
            elif token.type == DIV:
                self.eat(DIV)
                result = result // self.factor()

        return result


def main():
    while True:
        try:
            text = input('calc> ')
        except EOFError:
            break
        if not text:
            continue
        lexer = Lexer(text)
        interpreter = Interpreter(lexer)
        result = interpreter.expr()
        print(result)


if __name__ == '__main__':
    main()

Save the above code into the calc4.py file or download it directly from GitHub. As usual, try it out and see for yourself that it works.

将上面的代码保存到 calc4.py 文件中，或者直接从 GitHub 下载。像往常一样，尝试一下，看看它是否有效。

This is a sample session that I ran on my laptop:

这是我在笔记本电脑上运行的一个示例会话:

$ python calc4.py
calc> 7 * 4 / 2
14
calc> 7 * 4 / 2 * 3
42
calc> 10 * 4  * 2 * 3 / 8
30

I know you couldn’t wait for this part 😃 Here are new exercises for today:

我知道你已经迫不及待了:)这里是今天的新练习:

  • Write a grammar that describes arithmetic expressions containing any number of +, -, *, or / operators. With the grammar you should be able to derive expressions like “2 + 7 * 4”, “7 - 8 / 4”, “14 + 2 * 3 - 6 / 2”, and so on.
    • 编写一种 grammar，描述包含任意数量的 + 、-、 * 或/运算符的算术表达式。使用这种语法，你应该能够派生出“2 + 7 * 4”、“7-8/4”、“14 + 2 * 3-6/2”等表达式
  • Using the grammar, write an interpreter that can evaluate arithmetic expressions containing any number of +, -, *, or / operators. Your interpreter should be able to handle expressions like “2 + 7 * 4”, “7 - 8 / 4”, “14 + 2 * 3 - 6 / 2”, and so on.
    • 使用grammar，编写一个解释器，它可以计算包含任意数量的 + 、-、 * 或/运算符的算术表达式。你的解释器应该能够处理“2 + 7 * 4”、“7-8/4”、“14 + 2 * 3-6/2”等表达式
  • If you’ve finished the above exercises, relax and enjoy 😃 如果你已经完成了上面的练习，放松并且享受:)

我的答案（阅读完part5文字之后写的）：

expr : term ((PLUS|MINUS)term)*
term : factor ((MUL|DIV)factor)*
factor : INTEGER

# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, MUL, DIV,PLUS, MINUS, EOF = 'INTEGER', 'MUL', 'DIV', 'PLUS','MINUS','EOF'


class Token(object):
    def __init__(self, type, value):
        # token type: INTEGER, MUL, DIV, or EOF
        self.type = type
        # token value: non-negative integer value, '*', '/', or None
        self.value = value

    def __str__(self):
        """String representation of the class instance.

        Examples:
            Token(INTEGER, 3)
            Token(MUL, '*')
        """
        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self):
        return self.__str__()


class Lexer(object):
    def __init__(self, text):
        # client string input, e.g. "3 * 5", "12 / 3 * 4", etc
        self.text = text
        # self.pos is an index into self.text
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Invalid character')

    def advance(self):
        """Advance the `pos` pointer and set the `current_char` variable."""
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None  # Indicates end of input
        else:
            self.current_char = self.text[self.pos]

    def skip_whitespace(self):
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self):
        """Return a (multidigit) integer consumed from the input."""
        result = ''
        while self.current_char is not None and self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        """Lexical analyzer (also known as scanner or tokenizer)

        This method is responsible for breaking a sentence
        apart into tokens. One token at a time.
        """
        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()
                continue

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())
            
            if self.current_char == '+':
                self.advance()
                return Token(PLUS,'+')
            if self.current_char == '-':
                self.advance()
                return Token(MINUS,'-')

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            self.error()

        return Token(EOF, None)


class Interpreter(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # set current token to the first token taken from the input
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        # compare the current token type with the passed token
        # type and if they match then "eat" the current token
        # and assign the next token to the self.current_token,
        # otherwise raise an exception.
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """Return an INTEGER token value.

        factor : INTEGER
        """
        token = self.current_token
        self.eat(INTEGER)
        return token.value

    def term(self):
        result = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
                result = result * self.factor()
            elif token.type == DIV:
                self.eat(DIV)
                result = result // self.factor()

        return result

    def expr(self):
        """Arithmetic expression parser / interpreter.

        expr   : factor ((MUL | DIV) factor)*
        factor : INTEGER
        """
        result = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
                result = result + self.term()
            elif token.type == MINUS:
                self.eat(MINUS)
                result = result - self.term()
            
        return result

def main():
    while True:
        try:
            text = input('calc> ')
        except EOFError:
            break
        if not text:
            continue
        lexer = Lexer(text)
        interpreter = Interpreter(lexer)
        result = interpreter.expr()
        print(result)


if __name__ == '__main__':
    main()

Check your understanding.

检查你的理解。

Keeping in mind the grammar from today’s article, answer the following questions, referring to the picture below as needed:

记住今天文章的grammar，回答以下问题，根据需要参考下面的图片:

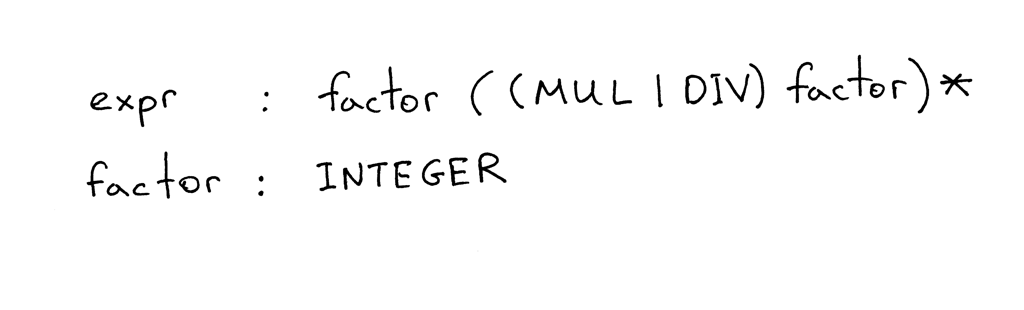
  1. What is a context-free grammar (grammar)? 什么是上下文无关文法？

应该如何理解「上下文无关文法」？ - Towser的回答 - 知乎 https://www.zhihu.com/question/21833944/answer/307309365
​

@徐辰 回答的特别好。
题主的主要疑惑应该在于：什么是上下文，上下文在哪里？为什么说这个文法上下文无关？
答案就是：在应用一个产生式进行推导时，前后已经推导出的部分结果就是上下文。上下文无关的意思的，只要文法的定义里有某个产生式，不管一个非终结符前后的串是什么，就可以应用相应的产生式进行推导。（从形式上来看，就是产生式的左边都是单独一个非终结符，即形如 S-> ...，而不是非终结符左右还有别的东西，例如 aSb -> ...）

这么描述有点儿抽象，我举一个自然语言的例子：
上下文无关文法：
产生式：
Sent -> S V O
S -> 人 | 天
V -> 吃 | 下
O -> 雨 | 雪 | 饭 | 肉

其中英文字母都是非终结符（SVO 分别表示主谓宾），汉字都是终结符。
这个文法可以生成如下句子（共 224=16 种组合，懒得写全了，简单写 7 种意思意思）：
｛人吃饭，天下雨，人吃肉，天下雪，人下雪，天下饭，天吃肉，……｝
可以看到，其中有一些搭配在语义上是不恰当的，例如“天吃肉”。其（最左）推导过程为：
Sent -> SVO -> 天VO -> 天吃O -> 天吃肉
但是上下文无关文法里，因为有“V -> 吃 | 下”这样一条产生式，V 就永远都可以推出“吃”这个词，它并不在乎应用“V -> 吃 | 下”这个产生式进行推导时 V 所在的上下文（在这个例子里，就是”天VO“中 V 左右两边的字符串”天“和”O“）。事实上，在 V 推出“吃”这一步，它的左边是“天”这个词，而”天“和”吃“不搭配，导致最后的句子读起来很奇怪。

那上下文有关文法呢？产生式可以定义为（其中前两条产生式仍是上下文无关的，后四条则是上下文有关的）：
Sent -> S V O
S -> 人 | 天
人V -> 人吃
天V -> 天下
下O -> 下雨 | 下雪
吃O -> 吃饭 | 吃肉

可以看到，这里对 V 的推导过程施加了约束：虽然 V 还是能推出”吃“和”下“两个词，但是仅仅当 V 左边是”人“时，才允许它推导出”吃“；而当 V 左边是”天“时，允许它推导出”下“。这样通过上下文的约束，就保证了主谓搭配的一致性。类似地，包含 O 的产生式也约束了动宾搭配的一致性。
这样一来，这个语言包含的句子就只有｛人吃饭，天下雨，人吃肉，天下雪｝这四条，都是语义上合理的。
以”人吃饭“为例，推导过程为：
Sent -> SVO -> 人VO -> 人吃O -> 人吃饭
其中第三步推导是这样的：非终结符 V 的上文是“人”，因此可以应用“人V -> 人吃”这条产生式，得到“人VO -> 人吃O”。第四步也类似。

而 @范彬 回答的是语法的歧义性，这和 CFG 无关。最简单的例子：
假设有如下上下文无关文法：
S -> S1 | S2
S1 -> ab
S2 -> AB
A -> a
B -> b
那么对于 "ab" 这个串，一种推倒方式是 S -> S1 -> ab，另一种是 S -> S2 -> AB -> aB -> ab。前一种要把 "ab" 合起来，后一种要分开，这只是说明该文法有歧义，而不能说这是一个上下文有关文法。事实上，还有一些上下文无关语言是固有歧义的（能产生该语言的每一种上下文无关文法都有歧义）。

  1. How many rules / productions does the grammar have? 语法有多少个规则/产生式？

多个
图中有两个

  1. What is a terminal? (Identify all terminals in the picture) 什么是终结符? (识别图片中的所有终结符)

像MUL、 DIV 和 INTEGER 这样的token称为终结符
图中的终结符有MUL、DIV、INTEGER

  1. What is a non-terminal? (Identify all non-terminals in the picture) 什么是非终结符? (识别图片中的所有非终结符)

像 expr 和 factor 这样的变量称为非终结符
图中的非终结符有factor和expr

  1. What is a head of a rule? (Identify all heads / left-hand sides in the picture) 什么是规则的头部? (识别图片中所有的header/left-head sides)

一条规则中冒号左边的终结符是规则的head
图中的header有：expr和factor

  1. What is a body of the rule? (Identify all bodies / right-hand sides in the picture) 规则的主体是什么? (识别图片中所有的bodies/right-hand sides)

一条规则中冒号右边的一系列终结符和/或非终结符是规则的body

  1. What is the start symbol of a grammar? 语法的开始符号是什么？

第一条规则左侧的非终结符称为开始符号。
图中的grammar中，开始符号是 expr。

Hey, you read all the way to the end! This post contained quite a bit of theory, so I’m really proud of you that you finished it.

嘿，你从头读到尾！这篇文章包含了相当多的理论，所以我为你完成了它而感到骄傲。

I’ll be back next time with a new article - stay tuned and don’t forget to do the exercises, they will do you good.

下次我会带着一篇新文章回来——请继续关注，别忘了做练习，它们会对你有好处的。

Here is a list of books I recommend that will help you in your study of interpreters and compilers:

以下是我推荐的一些书籍，它们可以帮助你学习解释器和编译器:

  1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
    语言实现模式: 创建您自己的特定领域和通用编程语言(实用程序员)
  2. Writing Compilers and Interpreters: A Software Engineering Approach
    编写编译器和解释器: 一种软件工程方法
  3. Modern Compiler Implementation in Java
    现代编译器在 Java 中的实现
  4. Modern Compiler Design
    现代编译器设计
  5. Compilers: Principles, Techniques, and Tools (2nd Edition)
    编译器: 原理、技术和工具(第二版)

All articles in this series:

本系列的所有文章: