Today we’ll talk about unary operators, namely unary plus (+) and unary minus (-) operators.

今天我们将讨论一元运算符，即一元加号(+)和一元减号(-)运算符。

A lot of today’s material is based on the material from the previous article, so if you need a refresher just head back to Part 7 and go over it again. Remember: repetition is the mother of all learning.

今天的很多内容都是基于前一篇文章的内容，所以如果需要复习一下第7部分，再复习一遍。记住: 重复是学习之母。

Having said that, this is what you are going to do today:

话虽如此，这是你今天要做的:

  • extend the grammar to handle unary plus and unary minus operators 扩展grammar来处理一元加号和一元减号运算符
  • add a new UnaryOp AST node class 添加一个新的UnaryOp AST节点类
  • extend the parser to generate an AST with UnaryOp nodes 扩展解析器以生成有UnaryOp节点的AST
  • extend the interpreter and add a new visit_UnaryOp unaryop method to interpret unary operators 扩展解释器并添加一个新的visit_UnaryOp方法来解释一元运算符

Let’s get started, shall we?

我们开始吧？

So far we’ve worked with binary operators only (+, -, *, /), that is, the operators that operate on two operands.

到目前为止，我们只使用了二元运算符(+ ,-，* ,/) ，即对两个操作数进行操作的运算符。

What is a unary operator then? A unary operator is an operator that operates on one operand only.

那什么是一元运算符? 一元运算符是只对一个操作数运算的运算符。

Here are the rules for unary plus and unary minus operators:

下面是一元加号和一元减号运算符的规则:

  • The unary minus (-) operator produces the negation of its numeric operand
    • 一元减号(-)运算符将对其数值操作数进行求反
  • The unary plus (+) operator yields its numeric operand without change
    • 一元加(+)运算符对其数值操作数不做改变
  • The unary operators have higher precedence than the binary operators +, -, *, and /
    • 一元运算符的优先级高于二元运算符 + 、-、 * 和/

In the expression “+ - 3” the first ‘+’ operator represents the unary plus operation and the second ‘-‘ operator represents the unary minus operation. The expression “+ - 3” is equivalent to “+ (- (3))” which is equal to -3. One could also say that -3 in the expression is a negative integer, but in our case we treat it as a unary minus operator with 3 as its positive integer operand:

在表达式“ +-3”中，第一个“ +”运算符表示一元加运算，第二个“-”运算符表示一元减运算。表达式“ +-3”等于“ + (- (3))”，等于 -3。也可以说表达式中的 -3是一个负整数，但是在我们的例子中，我们把它当作一元减运算符，3作为它的正整数操作数:

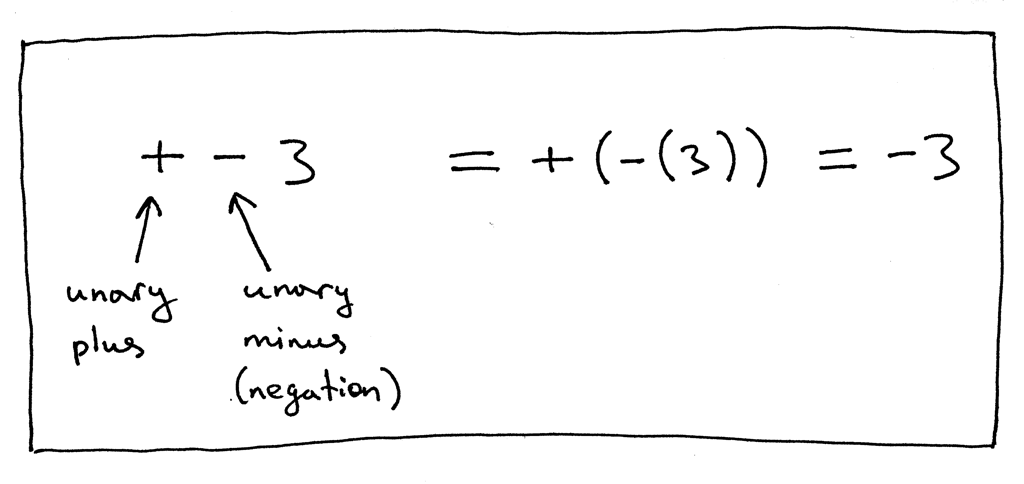
Let’s take a look at another expression, “5 - - 2”:
让我们看看另一个表达式：“5 - - 2”：

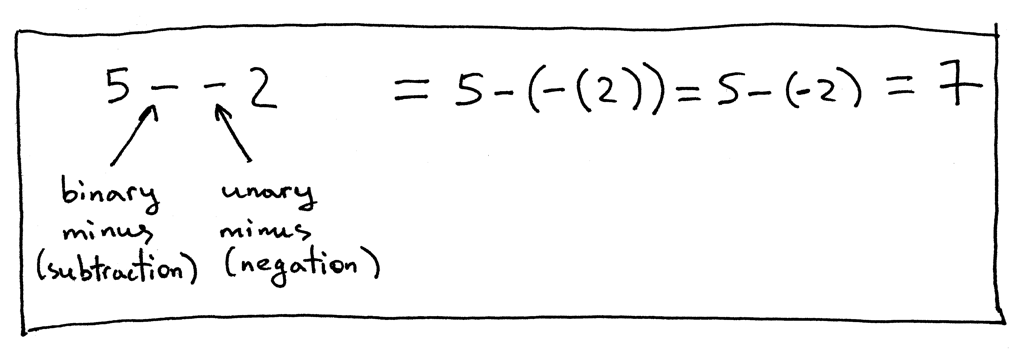
In the expression “5 - - 2” the first ‘-‘ represents the binary subtraction operation and the second ‘-‘ represents the unary minus operation, the negation.
在表达式“5-2”中，第一个“-”表示二元减法运算，第二个“-”表示一元减法运算，即负。
​

And some more examples:
还有一些例子:

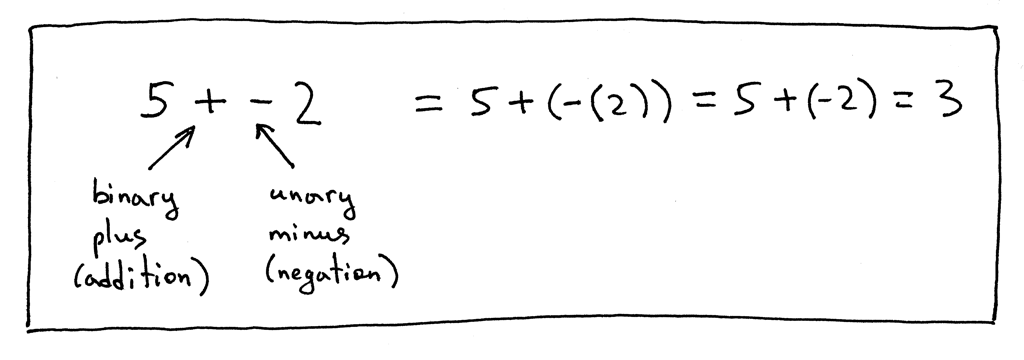
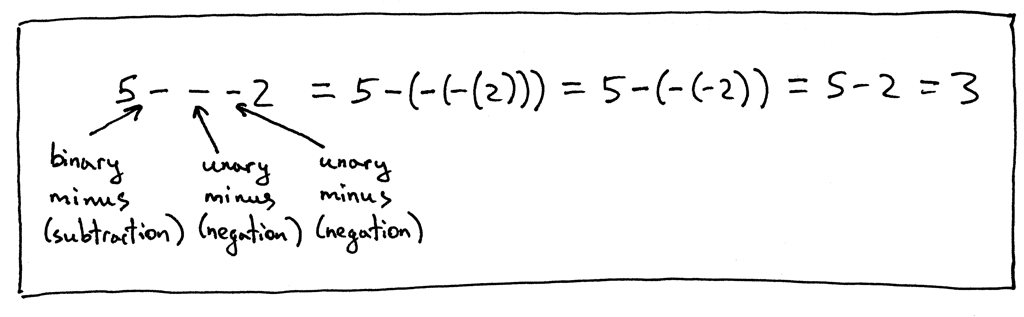
Now let’s update our grammar to include unary plus and unary minus operators. We’ll modify the factor rule and add unary operators there because unary operators have higher precedence than binary +, -, * and / operators.
​

现在让我们更新我们的语法，包括一元加号和一元减号运算符。我们将修改 factor 规则并在其中添加一元运算符，因为一元运算符的优先级高于二元 + 、-、 * 和/运算符。
​

This is our current factor rule:
这是我们当前的 factor 规则：

And this is our updated factor rule to handle unary plus and unary minus operators:
这是我们更新的处理一元加号和一元减号运算符的factor规则:

As you can see, I extended the factor rule to reference itself, which allows us to derive expressions like “- - - + - 3”, a legitimate expression with a lot of unary operators.
正如您所看到的，我将 factor 规则扩展到了引用本身，它允许我们派生“-- +-3”之类的表达式，这是一个合法的表达式，有很多一元运算符。

Here is the full grammar that can now derive expressions with unary plus and unary minus operators:
下面是完整的语法，现在可以用一元加号和一元减号运算符派生表达式:
​

The next step is to add an AST node class to represent unary operators.
下一步是添加一个 AST 节点类来表示一元运算符。

This one will do:

class UnaryOp(AST):
    def __init__(self, op, expr):
        self.token = self.op = op
        self.expr = expr

The constructor takes two parameters: op, which represents the unary operator token (plus or minus) and expr, which represents an AST node.
构造函数接受两个参数: op，表示一元运算符 token (加号或减号) ; expr，表示 AST 节点。

Our updated grammar had changes to the factor rule, so that’s what we’re going to modify in our parser - the factor method. We will add code to the method to handle the “(PLUS | MINUS) factor” sub-rule:
我们更新的语法对 factor 规则进行了更改，因此我们将在解析器中修改这个factor方法。我们将在方法中添加代码来处理“(PLUS | MINUS) factor”子规则:

def factor(self):
    """factor : (PLUS | MINUS) factor | INTEGER | LPAREN expr RPAREN"""
    token = self.current_token
    if token.type == PLUS:
        self.eat(PLUS)
        node = UnaryOp(token, self.factor())
        return node
    elif token.type == MINUS:
        self.eat(MINUS)
        node = UnaryOp(token, self.factor())
        return node
    elif token.type == INTEGER:
        self.eat(INTEGER)
        return Num(token)
    elif token.type == LPAREN:
        self.eat(LPAREN)
        node = self.expr()
        self.eat(RPAREN)
        return node

And now we need to extend the Interpreter class and add a visit_UnaryOp method to interpret unary nodes:
现在我们需要扩展 Interpreter 类并添加一个 visit _ unaryop 方法来解释一元节点:

def visit_UnaryOp(self, node):
    op = node.op.type
    if op == PLUS:
        return +self.visit(node.expr)
    elif op == MINUS:
        return -self.visit(node.expr)

Onward!

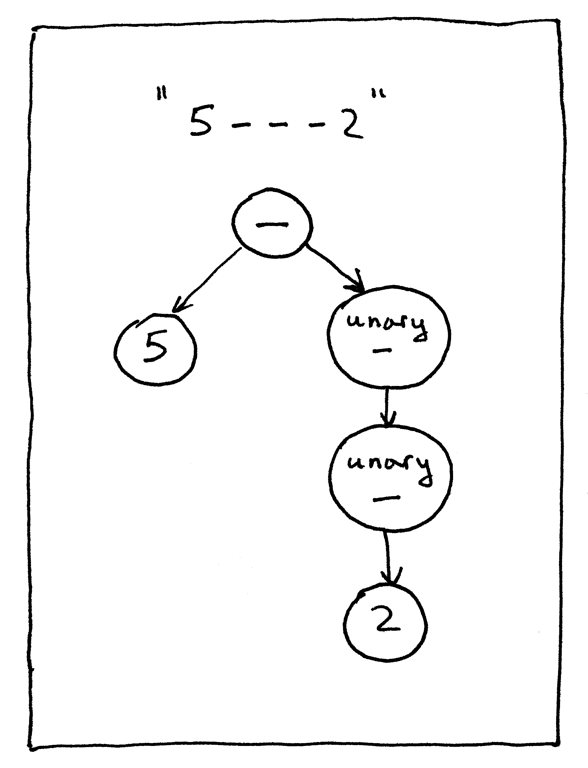
Let’s manually build an AST for the expression “5 - - - 2” and pass it to our interpreter to verify that the new visit_UnaryOp method works. Here is how you can do it from the Python shell:
让我们为表达式“5---2”手动构建一个 AST，并将其传递给我们的解释器，以验证新的 visit _ unaryop 方法是否工作。下面是如何在 Python shell 中实现它的方法:

>>> from spi import BinOp, UnaryOp, Num, MINUS, INTEGER, Token
>>> five_tok = Token(INTEGER, 5)
>>> two_tok = Token(INTEGER, 2)
>>> minus_tok = Token(MINUS, '-')
>>> expr_node = BinOp(
...     Num(five_tok),
...     minus_tok,
...     UnaryOp(minus_token, UnaryOp(minus_token, Num(two_tok)))
... )
>>> from spi import Interpreter
>>> inter = Interpreter(None)
>>> inter.visit(expr_node)
3

Visually the above AST tree looks like this:
从视觉上看，上面的 AST 树是这样的

Download the full source code of the interpreter for this article directly from GitHub. Try it out and see for yourself that your updated tree-based interpreter properly evaluates arithmetic expressions containing unary operators.
直接从 GitHub 下载本文解释器的完整源代码。您可以亲自尝试一下，看看您更新的基于树的解释器是否正确地计算包含一元运算符的算术表达式。
​

Here is a sample session:

$ python spi.py
spi> - 3
-3
spi> + 3
3
spi> 5 - - - + - 3
8
spi> 5 - - - + - (3 + 4) - +2
10

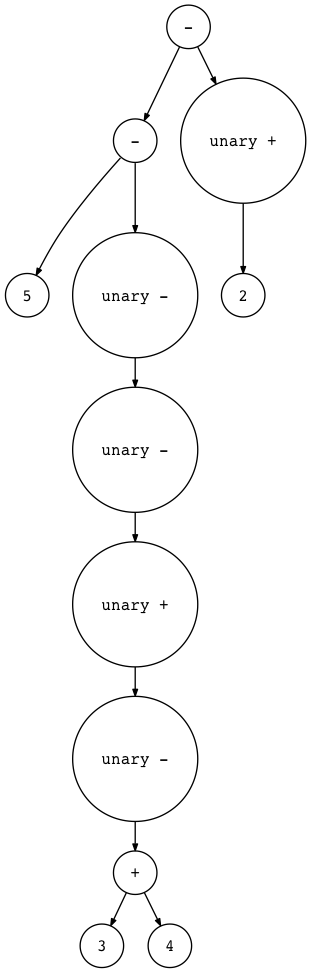
I also updated the genastdot.py utility to handle unary operators. Here are some of the examples of the generated AST images for expressions with unary operators:
我还更新了 genastdot.py 实用程序来处理一元操作符。下面是一元运算符表达式生成的 AST 图像的一些例子:

$ python genastdot.py "- 3" > ast.dot && dot -Tpng -o ast.png ast.dot

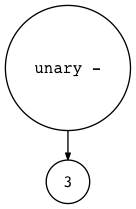
$ python genastdot.py "+ 3" > ast.dot && dot -Tpng -o ast.png ast.dot

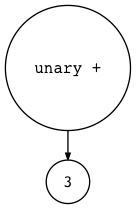
$ python genastdot.py "5 - - - + - 3" > ast.dot && dot -Tpng -o ast.png ast.dot

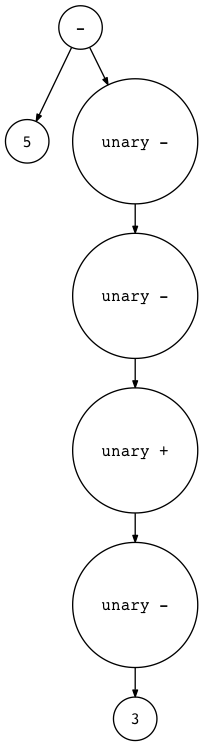
$ python genastdot.py "5 - - - + - (3 + 4) - +2" \
ast.dot && dot -Tpng -o ast.png ast.dot

And here is a new exercise for you:
练习：

  • Install Free Pascal, compile and run testunary.pas, and verify that the results are the same as produced with your spi interpreter.
    • 安装Free Pascal，编译并运行testunary.pas，验证结果是否和你的spi解释器的结果一样。

That’s all for today. In the next article, we’ll tackle assignment statements. Stay tuned and see you soon.
今天就到这里。在下一篇文章中，我们将处理赋值语句。请继续关注，稍后见。​

Here is a list of books I recommend that will help you in your study of interpreters and compilers:

  1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)
  2. Writing Compilers and Interpreters: A Software Engineering Approach
  3. Modern Compiler Implementation in Java
  4. Modern Compiler Design
  5. Compilers: Principles, Techniques, and Tools (2nd Edition)

If you want to get my newest articles in your inbox, then enter your email address below and click "Get Updates!"
以下是我推荐的一些书籍，它们可以帮助你学习解释器和编译器:

All articles in this series: